Data Structures

Prerequisite Topics:

You are expected know these topic before beginning the course.

• Comfortable writing and debugging programs 1 to 2 pages long
• Basic Java (types,control flow,etc.)
• Arrays(1D)
• Sequential Sort
• Insertion Sort
• Recursion
• Using objects
• Big-O worst case analysis

What is a Data Structure?

• A data structure is a format for storing multiple pieces of data or relationships between pieces of data. Some example of data structures are objects, arrays, linked lists, etc.

One important aspect of computer programming is checking how long the program takes to run and return the output. This is found using big-O analysis. Some factors that may affect the run time of a program include:

• Computer used
• Language of the program
• Compiler used
• Inputs
• Programmer abilities

How to analyze program runtime(Big O)

• Count number of operations executed instead of time elapsed
• The operation count of a program is a function of the input size
• Among inputs of the same size, count the worst case number of comparisons and the best case number of comparisons. Then this is used to find the Big O of the program by focusing on the large inputs and ignoring constants and other multiples.
• Big O notation is O(f), which means the Big O of a function that was found using worst case analysis.

Big O Analysis Review

• Since we are counting operations, the processor speed doesn’t matter
• Which operation do we count??
  • Most frequent / inner loop
  • Most time consuming
  • Inherent in algorithm, not programming language
• The number of operations depends on(“is a function of”) the number/size of inputs
  • Number of operations = f(input)
• Average case
  • Computing average cost:
    • What determines the cost?
    • For each such case, find the cost of that case(number of operations), and the probability of that case occurring
    • Sum the cost times the probability over all cases

Example :

Array Search code :

Input: double Array A, int n, double target
Output: boolean: Are any of the first n elements of A equal to the target value

for(i=0; i<n; i++){
  if (A(i) == target){
    break;
  }
}
return i < n;

• The above code scans through each element of array A, and checks one of the first n elements equals the target value. It returns true if a match was found within the first n elements and returns false if it was found outside of the n elements or not found at all.

Big O analysis of above code :

• Worst case : Match not found or match found at the end
  • number of operations = size of array

• Average case :

  \[\sum_{i=0}^n (p* \frac{1}{n}) = \frac{1}{n} \frac{n*(n+1)}{2} = \frac{n+1}{2}\]
• Assume a 50% chance of target not being found
  • If target is found, then there is an equal probability at each position
  • Average Cost = [P(found) * cost if found] + [P(not found) * cost if not found]

  
  
  

Linked lists

• Linked lists store an ordered list of data terms, all of the same type.
• Most of the time we don’t worry about what is 1st, 2nd, 3rd, etc., but it can be more efficient to care about “What comes next?”
• Each entry in the list contains a node. A node is a pointer from the current data element to the next.

The IntNode Class

public class IntNode{

  int data;
  IntNode next;

  public IntNode(int data, IntNode next){
    this.data = data;
    this.next = next;
  }
}

• The above code is an example of a class called “IntNode” which is used in linked lists. In the declaration statement of the IntNode called Next is a reference to an IntNode object. This code is just the code to create one node in the linked list.
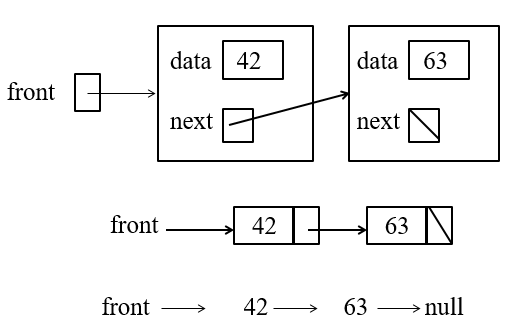
• The following is an example of a two-IntNode list.

• The front is where the data structure begins and points to the first node which contains the integer 42 as data. Then there is a pointer which points it to next node which has the integer 63 as data. After that the program will follow the next pointer to next node/data location, but in this case, the pointer points to null. This lets the program know that it has reached the end of the linked-list.
• Using this data structure is beneficial when compared to an array in program efficiency because it is much easier to add an element anywhere in the list.

Linked List Example Code

• IntLL Class example code - this is inherently just code for a linked list with 2 integer nodes.

public class IntLL {

	IntNode front;
	int size;

	public IntLL( ){
		front = null;
		size = 0;
	}
	public String toString( ){
		String result = "IntLL: [ ";
		for (IntNode ptr = front; ptr != null; ptr = ptr.next){
			result = result + ptr.data+" ";
		}
		result = (result + "]");
		return result;
	}
	public static void main(String[] args) {
		IntLL l1 = new IntLL( );
		IntLL l2 =  new IntLL( );
		l2.front = new IntNode(30, new IntNode(50,null));
		l2.size = 2;
		System.out.println(l1);
		System.out.println(l2);
	}
}

• The above is code that is for generating a linked list with integers as data. Specifically, the above code is a linked list with 2 nodes. So that means there are two data locations in the linked list. The unique thing about this code is that it is an object that represents the linked list. So, this list can be referenced in other codes easily.

• If the node was to have a string, then we would not change much, but just change all of the data types in the code from integer to string. It’s that simple!
• Below is the code for a node with string data

public class StringNode{
  String data;
  StringNode next;

  public StringNode(String data, StringNode next){
    this.data = data;
    this.next = next;
  }
}

• The code for a linked list with string data is similar to the code for the linked list with integer data, but we have to change the data types in the code from integer to string. The code for a two node string linked list is below.

public class StringLL {

	StringNode front;
	int size;

	public StringLL( ){
		front = null;
		size = 0;
	}

	public String toString( ){
		String result = "StringLL: [ ";
		for (StringNode ptr = front; ptr != null; ptr = ptr.next){
			result = result + ptr.data+" ";
		}
		result = (result + "]");
		return result;
	}

	public static void main(String[] args) {
		StringLL l1 = new StringLL( );
		StringLL l2 =  new StringLL( );
		l2.front = new StringNode("Mary", new StringNode("Joe",null));
		l2.size = 2;
		System.out.println(l1);
		System.out.println(l2);
	}
}

• Since the code for different types of lists are similar, we don’t have to specify if it is an integer list, string list, etc. We can use something called a generic list. The code for a generic list is shown below.

public class Node<E> {
 private E data;
 private Node<E> next;

 public Node<E>(E dat, Node<E> nxt){
data = dat;
next = nxt;
 }

 public E getHead(Node<E> head){
 E headData = head.data;
return headData;} ...

• This is the code to create the generic linked list object which can then be reffered to in another method or program with the code sample below.

Node<String> n1 = new Node<String>;
...
String name = n1.getHead( );

Operations that can be performed on Linked lists

• Insert at Head

• Remove the Head

• Insert after given node

• Remove at given node

• Find Last

• Traverse the List

• Insert at End

• Remove nodes greater than target

• Remove nodes greater than target

• Search for element x

Generics

• Linked lists can be made of several types of data, such as integers, strings, etc. However the data types throughout the list are the same. Instead of creating a linked list generation code for each type of object would be impossible because there are an infinite number of unique objects that can be created. This is why generics are used. I creates a generic code to create a linked list with any type of object, but with the same code.

• If you want to make a generic linked list that contains a primative type of variable(integer,double, float), you must use a wrapper class for that type of variable, such as Integer, Float, Double, etc.

• An example of the code for a generic linked list is shown below

public class List<T> {
Node<T> front;
int size;
public List() {
front = tail = null;
Size = 0;
}
void add(T data){}
void remove(T data){}
void update(T oldData, T newData){}
boolean contains(T data) { }
}
public class Node<T> {
T data;
public Node(T data, Node next) {
this.data = data;
this.next = next;
}
}

• The in basically a place holder for the data type of the data/node of the list. You can you use any letter in between the carots, but it can only be ONE character.

• The code for the implementation of the above linked list is below

/* Using generic List */
public static void main(String[] args) {
List<String> strList = new List<>();
strList.add(“First”);
}

Circular lists

• Circular lists are linked lists that have a front and the cycle through all of the entries. This means that the pointers go from the first data location to the last data location and then the pointer from the last location points to the first data location, inherently making a circle. Below is an example of a simple circular list.

• In the beginning of the linked list section, we learned how to add to a linked list by adding to the tail(‘end’), we can also add terms to the list at the beginning or the head. The example code to do that is below.

if(people == null){
 people = new Node(newName, null);
 people.next = people;
 } else {
 Node newNode= new Node(newName,
 people.next);
 people.next = newNode;
 }

• This can be useful in circular lists because then you can write the code to delete the head in your code, which will then create a circular list.

Doubly Linked lists

• A doubly linked list is a list where each node has a pointer to the next node and also the previous node. This can be useful in optimizing code when you have to search for the node which is right before another target node or going backwards through a list.

Recursion with linked lists

• Recursive code contains a base case where the code jumps out of the recursive cycle and also calls it’s self. This can be used to run a method again on it’s self several times or until a certain value is achieved.

Recursive operations that can be performed on Linked lists

• Insert new node at end of lists

• Insert new node after a target node

• Insert new node before a target node

• Delete the first occurrence of a target node

• Delete the node at a specified index

• Search for a node with target Data

Stacks

• A stack is a data structure which follows the rule of first in, last out. This means, what ever enters the stack first goes to the bottom, and the next entry get placed on top. Then, the stack is evaluated from top to bottom.

Terms for a stack
- Push -> add an element to the stack
- Pop -> remove the top element from the stack

Queues

• A queue is a data structure which follows the rule of first in, first out. This means, what ever enters the queue first is in the first position, and then everything else that is added after are added behind the first element in chronological order. The first element that is added to the queue is evaluated first, and then the next, and the next, and so forth.

Terms for a Queue
- Enqueue -> add an element to the queue
- Dequeue -> remove the first element in the queue

• Queues are represented by circular linked lists. This is because you add nodes after the tail and remove nodes from the tail.

Trees

• A tree is a data structure, where a tree contains nodes which have children which contain the next data values. A node in a tree can have any number of children.

Terms for a tree
- Root -> The node from which the tree originates.
- Subtree -> A tree which is located/rooted in a larger tree. Each node in a tree is a root of a subtree.
- Leaf -> A node with no children

Binary Search Trees

• A binary tree is a tree where every node in the tree has no more than two children.

• A binary search tree, is a tree where the data of the left child is less than the data of the parent, and the right child data is greater than the data of the parent.

• If input data for the tree is sorted, then the BST becomes similar to a linked list. It would not be beneficial to use a tree in this senario.

Traversing a Binary Search Tree

• There are two ways popular ways to traverse a binary search tree. Those are DFS(Depth First Search) and BFS(Breath First Search).

Depth First Search

• Depth First Search is a method of searching a BST which will visit every node at least once, in a recursive manner.
• This search is applied using recursion.

Pseudo Code for DFS
- Keep going to the left child until the next left child is null.
- Then return to the parent of that node and check if it has a right child.
- If it has a right child, the go right one node.
- Keep recursing through the entire tree by following these instructions.

• Traversing a BST with DFS has a O(n) efficiency, because the algorithm will visit every node in the tree at least once.

• Example code for general DFS function on a BST

//Test Comment
DFS(Node n){
  if(n == null){
    return;
  }
  else{
    if(n.leftsubtree != null){
      DFS(N.leftsubtree);
    }
    if(n.rightsubtree != null){
      DFS(n.rightsubtree);
    }
  }
}

Types of Depth First Search

• There are three types of Depth First Searches

  • Preorder

    Algorithm for Preorder
    - Visit node (Interact with node data)
    - Go left
    - Go right
    

  • Inorder

    Algorithm for Inorder
    - Go left
    - Visit node (Interact with node data)
    - Go right
    

  • Postorder

    Algorithm for Postorder
    - Go left
    - Go right
    - Visit node (Interact with node data)
    

• Generic code for Traversing a linked with the three different DFS

Breath First Search

• Breath First Search is a method of searching a BST which will visit every node at least once, but it will go level by level through the tree from the root to the leaves.
• This search is implemented by using a queue.

Pseudo Code for BFS
- Enqueue the root
- Dequeue one element and enqueue the children of that node.
- Keep recursing through the entire tree by following these instructions.

Balancing Trees

• A tree is considered balanced if the height of the right subtree of the node and the height of the left subtree of the node have a difference of zero or one.

• If a tree is not balanced, it can be balanced by rotations of specific subtrees within the tree. A great article about rotations from the University of Florida can be found by clicking HERE.

AVL Trees

• AVL trees are balanced binary search trees.